 |
| Schedule Analyzer | Brochure | Longest Path | Theory |
 The Theory behind LONGEST PATH Software.
The Theory behind LONGEST PATH Software.
The Problems with Total Float
In CPM theory, Total Float (TF) is the amount of time an activity can be delayed without delaying the overall project completion time. The TF of an activity is computed by subtracting its early finish from its late finish, or form its early start from its late start. Unfortunately, sometimes you get different answers depending upon which method you use. This is especially true with Hammock and Interruptible Activities.
The Total Float value of any given activity can also be affected by the setting of the CPM calculation setting of Interruptible/Continuous Scheduling. If you use the early dates (the default,) then the float value of interruptible activities will change with the changing of the scheduling method. If you use the finish date to calculate float, then hammocks will usually not present the expected float value.
The problem of float further compounds when you relate like activities together in a concept of ‘float path.’ In theory, activities directly related to each other with the same float value can be grouped together and considered as an entity called a “float path.” The most famous of these float paths is the “Critical Path” where the float value is equal to zero (or the lowest float value.) Unfortunately, this literal approach sometimes leaves out activities that would ordinarily be considered on the Critical Path simply due to activities having different work calendars.
Longest Path before LONGEST PATH Software
Primavera Systems, Inc., the makers of Primavera Project Planner (P3) and P6 scheduling software defines ‘Longest Path’ as the string of directly related activities that comprise the longest path from the data date to the last activity in the schedule. This definition does not concern itself with “float.” It includes activities that might otherwise be left out by the standard definition of Critical Path.
P6 calculates the longest path by identifying the activities that have an early finish equal to the latest calculated early finish for the project. P6 then identifies all driving relationships for these activities and traces them back to the project start date. Just like the CPM, the Longest Path is a process. It finds the last activity in the schedule and travels backward using the driving relationships.
LONGEST PATH Software
LONGEST PATH Software extends the theory of Longest Path to every activity in the schedule. Just as with Total Float, every activity in the schedule can be rated by its Longest Path Value.
Longest Path does essentially the same thing as Total Float, only it is computed in an entirely different process. Normally, it starts with every activity without a successor and calculates the time from early finish to early project completion and assigns that as Longest Path Value. It then progressively works the network ‘forward’ adding the current Longest Path Value to the relationship’s slack value and deriving the Longest Path Value of the predecessor activity. You also have the option of defining a Substantial Completion Activity and using this to define the end of the Longest Path instead of project completion.
Before you can compute the Longest Path Value, you first need to compute the slack value of every relationship in the network.
Slack
We are not surprised that you have never hear of the term “slack” as it concerns a CPM relationship. That is because we just made it up! This doesn’t mean that this is a trivial matter, it just proves that you can’t invent a thing until you first invent another thing (or you can’t get there from here.)
Slack is the amount of ‘unused’ time difference between the predecessor and the successor activities. This slack value has nothing to do with the float values or either of the two activities that it relates. It merely indicates how close each predecessor is to becoming the driving relationship for the successor activity.
Perhaps an example will suffice to explain my concept of slack. Note the following CPM fragnet (Figure 1.) Three activities lie in parallel between Task A and Task E. Task B is 6 days in duration; Task C is 4 days in duration; and Task D is 2 days in duration. The numbers outside of the boxes represent the slack of each Finish-To-Start relationship shown. For simplicity, all lags will be assumed to be 0.
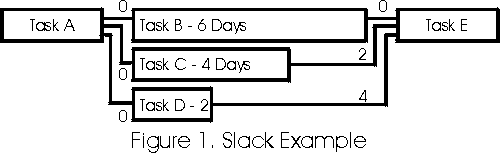
As the three activities in the middle (Tasks B, C, & D) each have only one predecessor (Task A,) the slack for each predecessor relationship must be 0. Each relationship is the controlling operation for each respective activity.
Task E, on the other hand, has three predecessors; Tasks B, C, & D. As Task B will take longer to complete than the other two below it, the relationship between Task B and Task E has 0 slack. In other words; it is the driving relationship. The relationship between Tack C and Task E requires 0 duration and has 2 days in which it can complete. The slack of Relationship Task C to Task E must be 2 days. Similarly, as the relationship between Task D and Task E requires 0 days but has 4 days to complete, then its slack value must be 4.
Longest Path Value
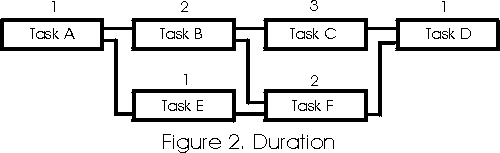
Now that we understand the concept of relative float in relationships (now called slack,) let’s use an example to show how Near-Longest Path can be calculated. Figure 2 shows another CPM fragnet that we will use to illustrate our concept. The numbers listed above each activity box are the activity’s duration. For simplicity, let’s assume that all relationships are Finish-To-Start with 0 lag.
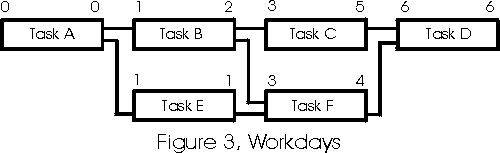
Using standard CPM principles, we calculate the Early Start and Early Finish hour numbers (see Figure 3.) The numbers listed above each activity box are the early start workday number (on the upper left) and the early finish workday number (on the upper right.)
What does it mean when we say that a relationship is a ‘Driving Relationship?’ We mean that it has a slack of 0. The relationship exactly fills the gap between predecessor and successor. In all cases, there should be one relationship with a slack of 0 (unless an activity constraint overrides this condition.) I note that no one has invented relationship constraints as of yet. I will leave this as an exercise for the student.
Returning to our original problem of obtaining Near-Longest Path activities, we have now defined the one measurement that allows us to qualify the level of longest path. The longest path contains all activities that are progressive successors of the finish activity that have a slack value of 0. Let’s just say that these activities have a Longest Path value of 0.
Figure 4 shows the results of comparing the Early Finish of the predecessor activity with the Early Start of the Successor. The numbers shown between the relationships are the result of evaluating the start of the relationship and its end. This value is called slack and represents how close the relationship is to becoming the driving relationship.
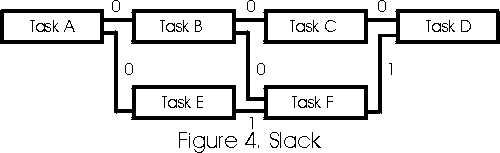
Now we are ready to calculate the longest path value of every activity in a CPM schedule. This value will represent the number of days that each activity has free before being included on the longest path.
The Longest Path value for each activity is calculated by progressively evaluating each predecessor activity, starting with the finish activity and adding the slack to the successor’s Longest Path value to give the current activity’s Longest Path value. In the case of multiple successor relationships, if the number derived is less than the current value then the new number is substituted for the old. Then we process every relation until all relationships have been evaluated. What could be easier?
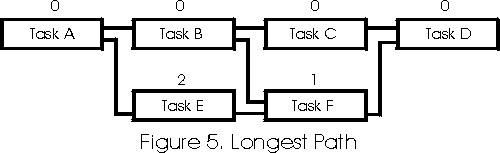
In our example, we start out by assigning the Longest Path value of “0” to the Finish Activity, Task D. We then work backwards through the CPM network adding the current Longest Path value to the slack value to derive the Longest Path value of the predecessor. If the number calculated for slack is higher than an existing value derived from some other relationship, we ignore that calculation and stick with the lower number.
Figure 5 shows the results of this Longest Path process. The numbers shown above each activity represent the Longest Path value for that activity. As expected, the Longest Path falls from Task A, to Task B, to Task C, and then Task D. We know this because their Longest Path value is “0.” Task F is the closest activity to the Longest Path without actually being on it with a Longest Path value of “1.” Task E has a Longest Path value of “2.”
LONGEST PATH Software then updates the schedule with these values. Since P6 doesn’t have a specific place in its database for Longest Path Values, we have to create on in the Custom Data fields. We create a numeric item called “PATH” and assign each activity in the schedule its own PATH value.
Longest Path Sequence
While we are replacing Total Float with Longest Path Value, we might also take a look at the secondary sort criteria, Early Start Dates. We need to order this schedule not by dates but by something inherently associated with the Longest Path, the order of logical sequences. This might pose a real problem if we didn’t just finish establishing this order in the process of computing the Longest Path Values for each activity.
In our example (Figure 5,) when we computed the Longest Path Values, we began with the last activity (Task D) and worked our way forward. Internally, we also kept a list of those activities as we processed them. The list for this example might look like the following,
Now, if we to reverse the order of this list, you would have a list of the logical sequencing for this schedule network. We call this the Longest Path Sequence.
We update the schedule by creating yet another Custom Data field called LSEQ and transferring the order number to each activity as well. In our example, Task A would have the LSEQ value of 1, Task E the LSEQ value of 2, and so on to Task D with the LSEQ value of 6. (Don’t forget that we reversed the list order.)
LONGEST PATH Software, Longest Path Value, and Longest Path Sequence are copyright Ron Winter Consulting LLC 2003.